Search the Community
Showing results for tags 'math'.
-
If you've ever been confused by a math problem, you belong here! Ask for help, or just discuss your confusion! Starting this thread because I stared at a problem for around ten minutes before I remembered that the Pythagorean Theorem existed. I felt very silly.
-
Ask your friendly neighborhood Lord Spirit anything you want to know about me, the universe and eveyrthing in-between. If you came from the subforum you know how this works.
- 23 replies
-
1
-
- lord spirit
- ama
-
(and 2 more)
Tagged with:
-
the "marioplex" is a number coined by matpat, describing all "fun", playable levels one could make in Mario Maker, thing is, MM2 (and 3,) are a thing now, so... let's do some math, shall we? how many total levels could one make in MM2? (and 3, should it come out.) Too complex? how 'bout SsbU, dlc included, with a difference between ai and human players? @The Last Fæ @The Bookwyrm
- 1 reply
-
- big numbers
- math
-
(and 1 more)
Tagged with:
-
From the album: The Geometric, Algebraic, & Mathematic
I made this for fun, I think -
All of the following is open to correction: We know that a sound wave can be represented by a sine equation, specifically y=a*sin(bx-c)+d. The opposite of a sound wave, the one that will cancel it out, can be represented by a phase shift equal to exactly half of that of the original sound wave, which is exactly the same as a simple inversion, or multiplying the equation by a negative. The collision of the sound waves cancels out the energy, but because the energy of the two hits at such a point that net motion of the air is negligible. Because the frequency of the wave is not changed, the two sounds are exactly the same to hearing, but still cancel each other out. It is generally only with intent that this can occur, as it is very hard to create the opposite of the sound by accident. In ROW, Navani creates anti-lights by using this inverse of the sound, so she is creating a sound that is exactly half a phase shift off of the rhythm of Odium. It makes a great deal of sense that doing this requires Intent, as it would be very common to find the anti-lights otherwise, or impossible to find at all. Something else that is interesting, is that light itself can be represented by the same equation y=a*sin(bx-c)+d, as it is an electromagnetic wave. Light can have the same equal-cancelling pattern, with two light waves that look the same cancelling each other out. This results in the bottom of the two images below, where the light cancels out in some places, and amplifies in other places. We know that the anti-lights annihilate each other like matter and antimatter, and that the sounds would as well. Now, I propose that if we positioned them correctly, the photon emissions from the two gaseous investitures would cancel each other out, though the air-warping around the anti-voidlight sphere(and possibly others) might interfere with that.
-
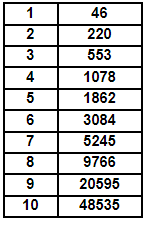
Reading Warbreaker and the amount of breath for each heightening, I noticed that the amount of breath followed some kind of exponential function. So I tried to find the math law that they follow I started by plotting the amount of breath versus the level (Figure 1) taking into account an error of 1% for each level. This is because it is written that the amount for each level is not exact, so I assume a value that increases as the level does. ↑Figure 1: BioChromatic Breath for each Heightening Then I tried different basic functions, but I found that it doesn’t follow those. Eventually I divided every amount by 50 (Figure 2) and by the level squared (Figure 3). ↑Figure 2: Figure 1 divided by 50 ↑Figure 3: Figure 2 divided by Level Squared With this i started to try again with this formula () and found values for A, B and C that approximated the curve. then i expanded the formula so the results approximated Figure 1, i got Eq. (1) Using OriginLab I plotted Figure 1, and fitted using Eq. (1). And i got Figure 4: ↑Figure 4: Figure 1 fitted using Eq. (1) The values for this formula are: Replacing the level we got this values: This aren’t very accurate, but they are very near, and may be the real values that are approximated in the books. Be aware that there is an unknown error to this values, they could be less or more Conclusion The most probable thing is that Brandon picked random values for each level, but it still was fun to try and find out this law. Replacing for an 11th heightening we get around 120000 breaths for it. If in the future there are more levels, and they follow this formula i would be very happy. Keep in mind they will most probably not follow this.
- 5 replies
-
11
-
- spoiler
- investiture
-
(and 3 more)
Tagged with:
-
I am mostly posting here to see thoughts on this, as I have been bothered by this for a while. I have been trying to find some sort of order in the levels of Heightening, or at least find an approximate formula to see if it follows any noticeable formula or such. Well checking the next numbers in the sequence after 10th using this https://alteredqualia.com/visualization/hn/sequence/, I have gotten 11th: 306,950 12th: 18,453,000 13th: 8,249,650 Showing that while this method works for 11th and 12th, it does not work at 13th and undergoes a massive drop. Which does not work with how Breaths and Heightening function. So we have to go another way. Well, knowing that the 8th has very, very little experimental data, and the data on it is likely wrong, we can look into it and say 8th: 7750 9th: 18750 10th: 56600 This, while not exact with the graph, does actually fit together with it all quite nicely. This also works with how the other levels are far more studied, so the approximations in the list are likely far more accurate. Though I know Heightening is basically just a made-up scale by people to give an estimation of when certain powers reach their peak, and does not actually exist, and furthermore, the values on the table are approximations. I just like doing math for fun. Additionally, just some math I did based on various factors, Susebron has at least 50,000 Breaths, in addition, he is given two to three Breaths a week from every God King over the course of 327 Years, likely numbering at 71,606 at the time of his ascension, and 75,428 by his marriage to Sisirinah. The formula would be 50000+78y, with y being the number of years. This assumes an average increase of 1.5 Breaths a day. Which is the average of gaining 1 or 2 breaths, as he uses one per week, thus to given two to three, means to increase by one or two.
- 2 replies
-
1
-
- awakening
- heightening
-
(and 1 more)
Tagged with:
-
Need any help with it? Come over here! Want to talk about it? This thread's for you! Want to hate on it? Go somewhere else because that's not what this thread is for. These people make excellent resources for help. Math/Calc: Chaos Classical Physics: Glamdring804 Micro/Nuclear Physics: Idealistic Mistborn Chemistry: Pagerunner Biology: Pestis the Spider Circuits: Silverblade5
-
A while ago it was discovered that the continent of Roshar exactly matches a 3d slice of a 4d Julia set. For those who didn't know, go to https://en.wikipedia.org/wiki/Julia_set and watch the video until you see Roshar. Now, I am not familiar enough with advanced maths myself to do this, but I imagine there is an equation for each Julia set and I was wondering if anyone would know if there's any way with the information we now know about the pure tones of Roshar to make even a guess at the equation for Roshar. I also know that if you type in Julia sets and music into google there's a scholarly article about how Julia sets can create musical pieces (think the rhythms of each shard, maybe?). I'm sure cymatics connects with all this too. Whatever you know or whatever you theorize (or whatever posts that have come up about this before) I'd love to hear it!
- 9 replies
-
1
-
- math
- rhythm of war
-
(and 1 more)
Tagged with:
-
A few days ago I solved a math problem posted by @Zelly, and that actually was the most fun I've had in quite a while. And I realized that it's also the only active learning I've done in a long time. So give me all your math problems. If you need help on an assignment or something pressing, make sure to say so, and I'll try to get to those ones first.
- 55 replies
-
- math
- i need more math
- (and 4 more)
-
Questioner 1 You said that moving people like that [Cognitive Shadows] or spren off-world, from Roshar is difficult. Brandon Sanderson Yes. Questioner 1 What about physically, say the Ones Above visit them, and they fly away? Brandon Sanderson So one of the things you'll have to be asking questions and theorizing on is what happens if you try to carry a spren around the planet. What happens to their Cognitive sense, right? So you're on Roshar, right? So on the Physical Realm what would happen-- Because on Shadesmar, you have a flattened version. So there are questions for you to be theorizing implicit in that. And one of them is, what happens, you cross a threshold circling the globe, your spren, what happens to them? Because-- Okay? This relates to the question you’re asking. Questioner 2 Wait wait, you have a three dimensional plane coexisting with a two dimensional plane? Brandon Sanderson Well, two dimensional is the wrong term, but basically... Questioner 3 Can you specify the mathematically projection used to create this? *laughter* Brandon Sanderson We'll try to give it to you eventually, but this is the sort of stuff that I do that Peter's like "Oh man..." *laughter* "Alright give me the math Peter." "Ahhh what do you mean? I'm not a mathematician." "Eh, y'know. You're close." It is very convenient to have a physicist and a mathematician in my writing group. Arcanum Unbounded Chicago signing (Dec. 6, 2016) I know that there's gravity and whatnot because when people jump into the bead ocean they fall, and I'm 99% sure you can die in shadesmar (I mean, what's the point of weapons), so with those bases covered, is it possible to die from falling in shadesmar? I think you could, but there are problems with that. It's 2D(somehow, "not exactly") so maybe a different dimension is missing? Maybe assuming that height is the missing one is wrong, but.... I dunno. There's depth to the oceans, height to fly, so maybe length and width are more like one dimension? He says it's flat so... This paragraph was kinda a waste off time?
-
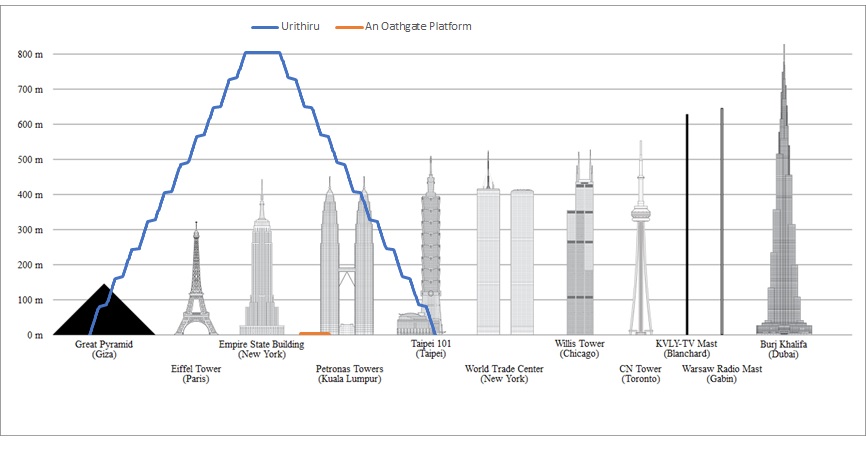
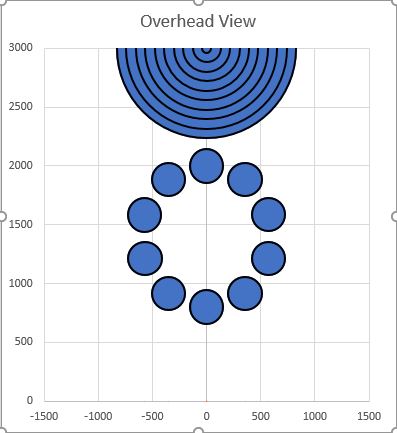
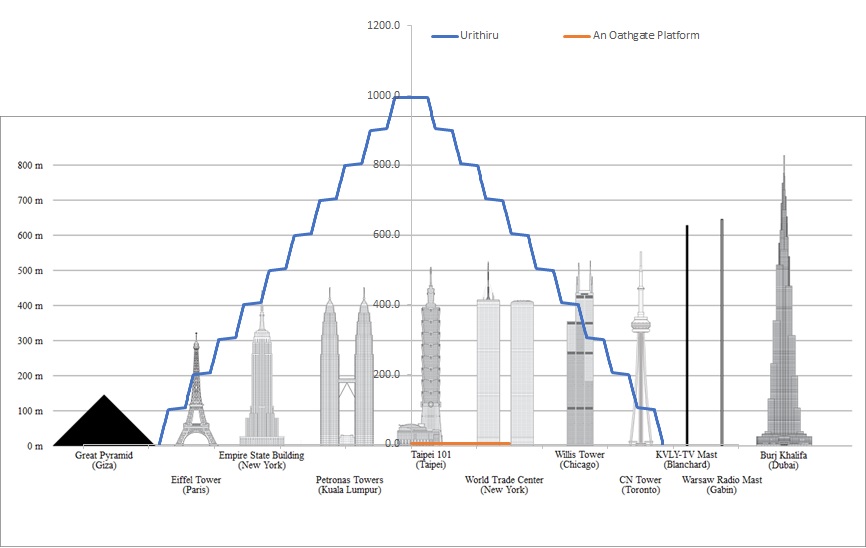
EDIT: Updated with some suggested numbers from the thread It is a little hard to grasp the scale of the tower city. Even Shallan can't capture it on the page! (To talk about that issue and whether it is driven by scale, psychology, or magic, see this thread.) Here are all of the physical descriptions we have of Urithiru. (If I've missed something you consider important, include a quote and I'll add it to this post. My chapter 87 quote is incomplete at the moment.) Summary: There are 10 tiers of 18 levels each, seemingly carved into the mountain. Each level is larger than the one above it, at least by the width of a balcony. The whole thing looks like The roof of the top level is ~100 yards across. The lowest level has a large plateau in front with the 10 oathgate platforms The oathgate platforms are raised 10 feet over surroundings, and are large enough to hold three armies worth of Everstorm survivors The lowest level also has large gardens/farms surrounding it. Assumptions: We have to make a lot of these. I'll update them as we get more information, or as others make convincing arguments, but for now let's go with: A Rosharan yard is close to 1 meter. Each balcony is 1.5 meters wide. Each new tier extends 20m 50m past the bottom of the one above, to accommodate gardens. Each floor is 4.5m 5.5m high, including the thickness of stone that supports the floor above. 20,000 people crowded onto the oathgate plateau at the end of WoR. (Does someone have a better number for this?) They pack closely but don't stab each other, about ~4 people/sq meter. This gives us an 80 meter diameter platform. The plateau is described as several hundred yards across, so we'll assume 300m for now. Conclusions: Using these numbers, we get a tower that is 1.5km wide at the base, and 1km high. Here's how that looks when compared to tall buildings on Earth (modified from this image on Wikipedia). A circular arrangement of ten 300m Oathgate platforms has an inner diameter of ^700m, and an outer diameter >1300m. To my mind, these are probably underestimates. As has been mentioned, Burj Khalifa is the tallest building on earth at 830 meters, and it has 160 floors to Urithiru's 180. At 4.5m per level+ceiling, I don't believe that our assumed thickness of stone has the structural integrity to hold up that massive a structure when it is filled with tunnels and cavernous spaces. Yes, surges could augment that strength, but I'm skeptical of a fabrial that would function to keep the city standing for millenia. I think we need to add more thickness to these load-bearing floors, and probably more width to the tiers. But before I modify the above assumptions, I'd like to see what the rest of you think. EDIT: Here is a perspective view of the tower and the oathgate complex. There is some disagreement in the thread about the arrangement of oathgates relative to the city, so I've included three versions here. Please comment to make your case for the arrangement you think is correct (one of these, or something different). Previous images:
-
There's been a fair amount of discussion about steel compounding on these forums as one of the most exciting forms of Twinborn. The general consensus (with support from Word of Brandon: wob.coppermind.net/events/93-odysseycon-2016/#e2695 ) is that a steel compounder could feasibly run at incredible speeds while being magically protected from many of the consequences for an extended period of time. So I decided to do the math on what it would look like for a steel compounder running at 10x normal speed (well within what Bleeder does in Shadows of Self, I think). Here's what I found: Imagine our Steelborn throwing a ball. Now, an ordinary person throwing a ball has their arm swing through a distance (call it 1 m) in a certain time and releases with a certain final velocity (call it 25 m/s for fairly ordinary humans - thats ~50 mph). Now, our Steelborn is moving 10x as fast, which I take to mean he takes 1/10 the time from start of throw to release. That implies he has 10x the release velocity (also what we expected). But he accelerated a ball to 10x the speed in 1/10 of the time of an ordinary human and acceleration = velocity/time (for constant acceleration of an object from rest, a decent approximation here), which means the Steelborn's ball has 100x the acceleration. F = ma, so either the ball had 1/100th of the mass, or our Steelborn applied 100x the force. Option 1: Changing strength Let's assume the ball's mass didn't change for now. Our Steelborn needs to apply 100x the force, which means our Steelborn needs to be 100x as strong as normal. It gets better. Our Steelborn has 100x the strength of an ordinary man and can run 10x as fast. Power = Force x Velocity, which means our Steelborn has 1000x the power output. If an ordinary human can output 300 Watts, our Steelborn can output 300 kW, or 400 horsepower. Of course, with 100x the strength, our Steelborn will need his tendons, ligaments, bones, etc. reinforced by 100x to avoid his enhanced strength tearing himself apart (see WoB above). Human skin normally has about 20MPa tensile strength, so a 100x increase puts us close to Kevlar's 3000 MPa tensile strength. His maneuverability with A-steel remains unaffected, though. There's no reason to assume his Steelpushes have enhanced strength, so he can't Push a coin any faster or Push himself off a skyscraper any quicker. (F = ma.) But the truth is, he hardly needs this. With 10x throwing speed, an ordinary 25 m/s pitch turns into a 250 m/s projectile (9mm pistol rounds travel at ~300 m/s, or ~1000 fps). With 20 bullets a throw and assuming he can get off 5 throws/sec, that means he is putting out the equivalent of 100 pistol rounds/second. (World War II machine guns fired ~10 rounds/sec.) He'd have to be aware of the recoil, though: he's not any heavier to absorb it! It's not all upside, though. Even with 10x the top speed and 100x the strength, our Steelborn is limited by the friction between his feet and the ground, which hasn't changed. Unless he can push off of something, he can't accelerate (or turn) at anything more than about 10 m/s^2. If he's moving at 10x an ordinary run speed of 4 m/s, and remembering that turning radius = velocity^2/acceleration on turns, we have turning radius = (40 m/s)^2/10 m/s^2 = 16 m. No hurtling around tables for him. Actually, I don't think he would run at all. With 100x the strength, each footfall would propel our Steelborn high into the air. I suspect he would move like astronauts walking on the moon instead. Option 2: Changing mass + gravity But all that doesn't match up with what Bleeder does in Shadows of Self. So instead of assuming that our Steelborn gets stronger, let's assume that our Steelborn's mass decreases to 1/100th of normal instead. 50 kg -> 0.5 kg. Additionally, the acceleration due to gravity must increase by 100x to leave the total force due to gravity unchanged to prevent him from bouncing high into the air with each step. Now, our Steelborn has the same strength and the same amount of traction (since he has the same weight as before) but 1/100th of the mass. F = ma, so that gives him 100x the acceleration. Hairpin turns are no problem: running at 40 m/s he has the same turning radius as an ordinary human running at 4 m/s (since turning radius = velocity^2/acceleration = 4^2/10 = (4x10)^2/(10x100)). Jumping is fine too: our Steelborn has 10x the takeoff velocity but 100x the downward acceleration. Jumping height = v^2/2g, so the effects cancel, leaving him able to **jump the same height as an ordinary human**. However, air time = 2*v/g, so he has 1/10th the air time, which is again what we expect. His maneuverability with A-steel is enhanced too. There's no reason to assume his Pushes have changed strength, so F = ma says with 1/100th the mass, his Pushes give him 100x the acceleration. The increased gravitational acceleration won't cause problems because the total gravitational force is unchanged. Additionally, he no longer needs Kevlar skin, as he hasn't gotten any stronger. Since his body has so little mass, his insane accelerations will result in the same forces on him as usual. He won't black out either. Clearly, the mass reduction and gravity enhancement must extend to the Steelborn's clothes, guns, coins, etc. Otherwise, carrying a 1 kg pistol when he himself has a mass of only 0.5 kg would reduce his maneuverability to 1/3 of expected, but we see Bleeder think nothing of Steelrunning with pistols. The problems begin, however, when we consider him throwing something. What happens when coins leave his hands and return to normal mass? I see three scenarios: 1. Coins return to normal mass but velocity unchanged. They increase in both momentum (p = m*v) and energy (KE = 1/2m*v^2). This gives him tremendous firepower: he can throw coins at 10x ordinary speed and 10x the rate, exactly as described above. His pistol rounds travel at 10x speed too: muzzle velocity = sqrt(2*d*a), so since 1/100th the mass -> 100x the acceleration by F = ma, bullets have 10x the muzzle velocity. To top it off, he's immune to bullets: incoming bullets are reduced to 1/100th of their mass upon hitting him. 2. Coins are reduced to 1/100th speed. This satisfies Conservation of Momentum: p = m*v, so if mass increases by 100x to return to normal, velocity decreases to 1/100th. Since KE = 1/2m*v^2, their energy decreases to 1/100th (losing energy is more permissible than gaining it at least!). His coins are reduced from 250 m/s on leaving his hand to 2.5 m/s - 1/10th of an ordinary throw speed. This affects bullets too: they have 10x the muzzle velocity initially, but as soon as they stop touching him, they are reduced to 1/100th of the speed. The net effect is to reduce a 300 m/s pistol bullet to a 30 m/s one. Our Steelborn's problems get even worse when we consider bullets striking him: they are suddenly accelerated to 100x their velocity, satisfying Conservation of Momentum, but resulting in a 100x increase in bullet energy since KE = 1/2m*v^2. 3. Coins are reduced to 1/10th speed. This satisfies Conservation of Energy: KE = 1/2m*v^2, so a 100x increase in mass is balanced by 1/10 velocity, but doesn't satisfy Conservation of Momentum. His throwing speed is unaffected, since coins leave his hands 10x faster than normal, but then are reduced to 1/10 speed, or normal throwing velocity. The same applies to pistol bullets. Bullets striking him are reduced to 1/100th mass but have 10x the velocity, leaving their energy again unchanged. Of all the options, I think 3 fits the best. Our Steelborn cannot throw or shoot at crazy speeds with F-steel - though he can still put out huge numbers of bullets and Push them to deadly speeds with the help of A-steel. Now that we have established how he (roughly) interacts with objects, much of his power depends on how far this field extends. Does it affect a bike he rides? A car he drives? A train? I suspect the explanation invokes his Connection to an object and the object's own Identity, but I see no evidence for how. The TL;DR The best match with Shadows of Self is that you can't change your strength with F-steel: you obtain crazy speeds by reducing mass and increasing gravity while permitting your muscles to operate at higher speeds. (This pairs well with F-Iron: both manipulate mass.) Anything you throw is reduced in speed and increased in mass when it leaves your hands. This gives enhanced maneuverability and speed without crazy firepower. Thoughts?
-
I came up with this sequence in math class a couple of months ago when we were asked to make up a rule, write down a sequence using that rule, and pass them around the room. When you figured out the rule you were supposed to trade with someone else and try to figure out that one. Afterwards the professor put the sequences that stumped people on the board and we figured them out together. However the following sequence which I made wasn't solved and stumped the whole class, professor included. So here it is: 0,0,3,16,45,120,280,624,1323,2720... Try to figure the rule for this sequence.
-
Edit 3: Here's a quick look into my most recent progress - labels over targets, a more detailed HUD, and several physics tweaks. I'll edit what I can from the original post, but there's a lot of physics discussion in the replies that I highly suggest you read. Jofwu and I've discussed other possible relationships between Force and Distance, and there's a bit of a strange one that he came up with a while ago: Allomantic Force ∝ e ^ -d/D where d = distance and D = 16 When the target is right next to the Allomancer, e ^ -d/D approaches 1 and the AF approaches its maximum. When the target approaches an infinite distance away from the Allomancer, e ^ -d/D approaches 0 and the AF approaches 0. This strategy looks very similar to the linear relationship but avoids its icky discontinuity at the max range of the push. I like it a lot. For comparison, you can see all three Force-Distance relationships together here. Edit 2: Following Jofwu's footsteps, I had a conversation with /u/Phantine on reddit and am reconsidering how distance affects the Allomantic Force. I was originally confident in an inverse square relationship between Allomantic Force and the distance between the Allomancer and target, but through testing, a *linear* relationship has better handling and feels more reminiscent of Allomancers' movements in the books. I've added both as options in the game: The Allomantic Force is proportional to the inverse of the square of the distance between the Allomancer and the target When the target is right next to the Allomancer, the Allomantic Force approaches infinity. When the target approaches an infinite distance away from the Allomancy, the Allomantic Force approaches 0. The Allomantic Force decreases linearly with the distance between the Allomancer and the target. When the target is right next to the Allomancer, the Allomantic Force is at its maximum. When the target is at the max range (arbitrarily at 50 meters), the Allomantic Force is 0. I've also added the option to control the strength of your push through two control schemes: The player sets the *percentage* of the maximum possible force they can push with, or The player sets a *constant force* to try to push at, if possible. Edit 1: If you want to play the current build of the game, you can find it here on my GitHub. Aside from that, I've looked back at [8], @digitalbusker's post and see I misunderstood it a bit. I've re-read it and realized that I agree with it much more than I thought I did originally. In one paragraph, they said, This sounds just like the Allomantic Normal Force idea I used in the game. If you push on a target and the target can't move, the target pushes back on you as if there were a long, tangible line between you and the target. In this way, the ANF does work somewhat like an elastic collision. I did some more testing in the game and anything that involved directly manipulating velocities of the target or Allomancer worked poorly. I feel like sticking to forces rather than energy is the right way to go. Table of Contents I: Introduction I-a: My intent I-b: Current game progress & Videos I-c: Referenced forum posts I-d: Definitions II: Force, mass, and acceleration of a push III: Anchors and the pole analogy IV: Math V: Summary & Final points Part I: Introduction Over the summer I’ve been rereading Mistborn and have been thinking about the mechanics of Allomancy. I decided to have a go at recreating the physics of Ironpulling and Steelpushing in the Unity physics/game engine. I don’t intend on actually creating a game to sell (that’d be a bit illegal), so this is mostly an endeavor for personal fun. What follows is my current progress on the game as well as my current thoughts on the math and physics of Pushing and Pulling. Part I-a: My intent My goal is to take what Brandon describes in his books and do my best to create a working model of them in the Unity engine. My purpose in posting this here is to record my thoughts so I can be internally consistent, encourage discussion, and improve the game’s mechanics with your suggestions and criticisms. I don’t expect to perfectly recreate Allomancy as Brandon describes it in the books because there are some things with little connection to real-world physics (such as Feruchemical weight). I’ll try to give the pros and cons for all my decisions. If you disagree, tell me! I’ve been in my own personal bubble while making this, so I’d love some external input. Part I-b: Current game progress & Videos So far, I’ve implemented most of the physics and fundamentals of Ironpulling and Steelpushing. Here are some short videos: The setting: The sandbox I use for testing is based on Luthadel. There are metal poles stuck in haphazardly-placed buildings, and a few windows with metal frames/latches. At the intersection are metal objects of various masses, including coins, ingots, and 16-ton steel blocks. Blue metal lines: When the player (the grey sphere) begins passively burning metal, they see blue metal lines pointing towards nearby metal sources. The wider the line, the heavier the metal, and the brighter the line, the closer the target. Basic pushing/pulling: The player can “target” a metal. They can then push or pull on that metal. They can increase or decrease the strength of the push, as indicated by the wheel near the bottom. They can target multiple metals simultaneously (as indicated by the bright blue number beneath the wheel). Pull targets vs. Push targets: The player has separate targets for pulling (indicated by blue) and pushing (indicated by red). When the player pushes or pulls with specified push targets and pull targets, the player only pushes on the push targets and only pulls on the pull targets. If the player only has pull targets or only has push targets, they can push and pull on any target. Pushing/pulling with coins: The player can throw, drop, and pick up coins. The number in the lower right corner indicates the number of coins in the player’s pouch. Flying around Luthadel: It’s a bit tricky, but the player can fly between buildings by pulling on metal latches and pushing on coins. Some things are still a bit buggy, namely the camera, coin physics, and width of the white part of the blue/red line pointing at a target while pushing. Part I-c: Referenced forum posts Many of the ideas used in the calculations come from the work previous Sharders have done on making sense of Brandon’s magics. Here are some that I used, which I recommend to anyone interested in the physics of Allomancy: When I use specific ideas from these threads, I’ll mark it with a [#]. Other threads I found interesting: Part I-d: Definitions Key statements are italicized. Key terms are written in bold for their first appearance. Push – unless I specify otherwise, I’ll simply say “push” instead of “push/pull” to refer to the math of both steel and iron. It’s a lot easier to read while still means the same thing. All physics and rules of a pull are the same as a push, just in the opposite direction. Target – the metal that an Allomancer is currently pushing on. Coins are often a target. Distance – the distance between an Allomancer and their target. Anchor/anchored – a target is an anchor if it does not move. A lamppost, a coin stuck on the ground, and a metal roof would all be anchors. Note that the metal is the anchor, not the nearby wall/ground/stone. A target is unanchored if it is moving freely with no resistance. A target is partially anchored if it meets some resistance but is not fully anchored (i.e. a coin skidding on the ground). Allomantic Force (AF) – the force that an Allomancer directly exerts on a target while pushing. Equal in magnitude to the force that the target directly exerts on the Allomancer while pushing. The Allomantic force does not change if the target is anchored or unanchored. Allomantic Normal Force (ANF) – the force that is exerted on an Allomancer or target as a result of the opposing target or Allomancer's push or pull by the surrounding ground, walls, etc. I'll discuss this down below. Essentially, it's what makes anchored targets give that extra strength to your push. Now, let's jump into the physics of Allomancy. Part II: Force, mass, and acceleration of a push When Allomancers in the books refer to “weight,” they almost always mean mass. [1] Let’s ignore Feruchemical weight for now. When an Allomancer pushes on a target, the Allomancer exerts a force on the target that is equal and opposite to the force that the target exerts on the Allomancer. It’s F = ma, it’s Newton’s third law, and if anything else were the case, the physics of Mistborn would be far too distant from our world for a good simulation. This explains one of the core features of pushing and pulling: If you push on an object heavier than you, you will accelerate more than it (and vice-versa). You push on a coin out in front of you. The force is the same between you and the coin, but the coin has less mass, so it accelerates more than you. The coin goes flying, but you hardly move. Likewise, heavier objects (like cars) have more mass than you, so you accelerate more than them. The previous statements are most apparent with an Allomancer and target in free-fall or space, where the Allomancer and target (such as a coin) won’t be anchored by anything (such as the ground). When the Allomancer or target are anchored by a wall or the ground, things get complicated. Part III: Anchors and the pole analogy In the books, if an Allomancer is falling through the air, throws a coin downwards, and starts pushing on it, the Allomancer doesn’t feel much while the coin is falling through the air and unanchored. The Allomancer pushes on the coin, but their acceleration from the push is not enough to stop their fall. Once the coin hits the ground and stops moving, the Allomancer suddenly “can get a stronger push” and decelerate more strongly. Here is my interpretation: Pushing against an anchored coin on the ground has a similar effect as holding a long pole and physically pushing against the ground. The Normal Force due to the Allomantic Force (Allomantic Normal Force, or ANF) that the ground/wall/etc. exerts on the target is transferred to the Allomancer. If you held a long vertical pole and pushed down on the ground, the ground would push back on you and the pole. If you tried to push the pole into the ground, the ground would resist, and you could climb upwards relative to the ground. Allomancy mimics this effect. When pushing on the coin, it is like you are physically connected to the coin. If something resists your push, you experience that resistance. It's just like you're literally pushing against the coin with your fists. If the coin's in the air, hardly anything happens. If the coin's on the ground, the ground resists. I drew some free-body diagrams that hopefully help explain what I’m saying. In these, an Allomancer and coin are falling down. The Allomancer is pushing on the coin. Let me discuss two of the other theories as to how Allomancers get stronger pushes from anchored targets: When the coin is airborne, the allomancer is only pushing on the mass of the coin. But when the coin is anchored to the planet, they are also pushing on the mass of Scadrial/the ground around the coin, which causes the Allomancer to accelerate more. [not a quote, but the concept taken from 1] I’ll get into how mass affects the force later in the math section, but I want to now make something clear. With my interpretation, Allomancers push on the mass of metal, not the combined mass of metal and nearby non-metal (the planet). When pushing against an anchored coin, the Allomancer is only indirectly pushing on the ground – they are pushing on the coin, which pushes on the ground, which resists back on the coin, which resists back on the Allomancer – similar to holding a long pole and pushing on the ground. An Allomancer’s strength is the amount of kinetic energy they can add to the system of the coin and allomancer. When the Allomancer pushes on an unanchored target, that kinetic energy is distributed between the two, proportionally to their masses. But, when the target is stationary, their velocity is zero, so all of the kinetic energy is given to the allomancer (and vice-versa). [paraphrased from 8] I like this explanation. Honestly, I may agree with it more than with my own ANF theory. I tried it out, but it was a lot more difficult programming-wise than the ANF idea. Unity has easier force manipulation than energy manipulation, so I framed my theory using that. Energy is just force with extra steps. (See Edit 1) I’ll talk more about the Allomantic Normal Force and partially-anchored targets after the math in Part V. Part IV: Math Now, I’ll introduce the formula that I used to calculate the Allomantic Force. After that, I’ll describe each of the terms in detail. Allomancy is a lot like magnetism, so let’s start by looking at the formula for the magnetic force between two poles. In Allomancy, the “two poles” would be the Allomancer and target. Magnetic Force = Constant * q1 * q2 / r2 Constant – some constant that depends on the medium between the poles. q1and q2 – the magnitudes of the magnetic charges of the poles. r – the distance between the poles. The greater the charges, the greater the force. The greater the distance between the two poles, the weaker the force – and through the inverse square relationship, greater and greater distances cause much weaker and weaker forces. Now, the Allomantic Force: Allomantic Force = A * S * b * c1 * c2 / r2 (See Edit 2/3) A – some constant. This depends on how all pushes and pulls are described in the book and can be increased/decreased for overall stronger/weaker pushes. b – Burn rate. See below. S – Allomantic Strength. See below. c1 and c2 – the Allomantic Charges of the Allomancer and target. r – the distance between the Allomancer and target. Burn rate – the rate at which an allomancer burns their metals. For my purposes, burn rate is a range between 0 and 1, where 0 is “not burning at all” and 1 is “pushing as hard as you can,” possibly without flaring. I bound this to the triggers on a gamepad and to the scroll wheel on a mouse, which allow me to variably control the strength of a push using the burn rate. Allomantic Strength – the most magic-y of the all the components of the force. Some Allomancers are naturally stronger than others, perhaps by sDNA. Allomancers get better with training and experience. These factors get bundled into the Allomancer’s Allomantic Strength. The Allomantic Force is not proportional to the Allomantic Strength (see [3]). Rather, the Allomancer’s maximum burn rate is proportional to the Allomantic Strength. In this way, Allomantic Strength acts as a sort of limiter. Stronger Allomancers must be able to burn more metal faster for a stronger effect. I won’t incorporate this in-game. Allomantic Charge – Analogous to magnetic charge. Contributes to the Allomantic Force. A property of both metals and Allomancers. I recommend now reading [1], which has a very interesting theory on this. I’m not adhering to it completely, though. An Allomancer or target’s Allomantic Charge is a function of its mass. To make the mass relationships of Mistborn work, we need to satisfy a few factors: The more massive a target is, the stronger a push an Allomancer can get off of it. The less massive a target is, the weaker a push an allomancer can get off of it. “[Wax] shot outwards in a grand arc above the city, flying for a good half a minute on the Push off those enormous girders” (AoL ch 1 pg 34) [3]. “…the lamp was a good anchor - lots of metal, firmly attached to the ground - capable of pushing [Wax] quite high” (AoL ch 1 pg 32) [3]. Both of the targets in these quotes are equally anchored, but the girders are much more massive and provide a stronger push. I don’t have any direct quotes, but we know that Allomancers get less of a push from coins than they do from, say, enormous girders. The “heavier” an Allomancer is, the stronger their push. This argument comes from Feruchemical weight, not mass, but it nonetheless impacts Allomancy in the books, so I should bring it up here. While tapping weight, Wax thought, “with this incredible conflux of weight, his ability to Push grew incredible” (AoL) [2]. I can’t quite remember the context or quote, but I recall that one of Kelsier’s surprises about Vin was her Allomantic Strength/Charge was large “for her size,” implying that smaller/less massive Allomancers usually have less charge. It’s symmetrical with the target’s mass impacting the Allomantic Charge. It’s intuitive and makes sense. There should be some soft maximum cap and minimum cap to the force. If an Allomancer pushes off of an absolutely massive multi-ton solid block of gold, they shouldn’t be pushed into the stratosphere. Likewise, coins are very light relative to lampposts and roofs, but they still provide a reasonably strong push. This leads me to the most disgusting part of the math. What exact relationship do the masses have with the force? The relationship can’t be zero. If this were the case, mass would have no effect on the force, which I argued against. Also, an Allomancer could push on a “metal” with a mass of 0 and still get a push, which doesn’t make sense. The relationship can’t be linear. If this were the case, a target 10 times as massive as another would provide 10 times a push as the other, which doesn’t appear to be the case. If an Allomancer pushes first on a 30g coin and then on a 30kg metal block, the Allomancer would receive 1000 times more the force from the block than the coin. In the books, Allomancers push off of girders and roofs which are much heavier than 30kg, but they certainly don’t describe such a massive difference in forces from coins. That’s duralumin-levels of strength. I’ve tried out a lot of relationships. Logs, sum of logs, product of logs, and roots. Eww. My solution was to take the root of the masses of the Allomancer and target. Specifically, the, ah, sixteenth root. It provided a good combination of strong-enough pushes from light coins and weak-enough pushes from very massive targets that felt most similar to the books. The number 16 was arbitrary. I figured I might as well use Scadrial’s base number for legitimacy. If I used a more elegant root (i.e. the square root), coins provided practically no force, and massive targets still pushed to the stratosphere. Higher roots “level the playing field” more than lower roots. c1 = sixteenth root of (m1) c2 = sixteenth root of (m2) m1 – mass of Allomancer m2– mass of target Because of how roots work, we can also say that c1 * c2 = sixteenth root of (m1 * m2). Regarding the maximum to the force that an Allomancer can get from an extremely massive target: The heavier and heavier the target, the less and less the increase in force. No pushes to the stratosphere. I’m not actually sure if this is the case with roots, but it felt like it was: the lighter and lighter the target, the less and less the decrease in force. Coins are very light, but still provide a significant push. In the end, I’m not actually trying to figure out how mass affects the force in the books. I am fairly confident Brandon didn’t consider the exact relationship while writing the books. I’m just finding ways to emulate it in a physics engine. Part V: Summary & Final points And here’s the final, composed formula for the force an Allomancer experiences while pushing: Force on Allomancer = Allomantic Force + Allomantic Normal Force = Allomantic Constant * Burn rate * sixteenth root of (target mass * Allomancer mass) / squared distance between Allomancer and target (See Edit 2/3) + Allomantic Normal Force Burn rate is between 0 and 1. A Burn rate of 1 gives the maximum Allomantic Force. When target mass is 0 or the Allomancer mass is 0, the Allomantic Force is 0. The closer and closer the target is to the Allomancer, the greater and greater the Allomantic Force. Like other normal forces, if the target isn’t fully anchored (e.g. a coin sliding across the ground, or a thin metal rod that bends as you push on it), the Allomantic Normal Force ranges from 0 to the Allomantic Force, depending on how anchored the target is. This means that an Allomancer pushing on a perfectly anchored target will be pushed back with twice the force as a perfectly unanchored target, assuming they have the same distance. This last bit about the distance is key. If an Allomancer is falling through the air and throws down a coin, the coin quickly falls further and further down. The Allomantic Force quickly becomes very small. Only once the Allomancer falls further and is near the coin – now anchored to the ground – does the distance stay small enough for the Allomantic Force to be large enough for a long enough time to scale a building. Friction (and air resistance) can also be a normal force, in this context; any (normal component of a) force that resists the Allomantic Force can be an ANF. Gravity, too, can be an ANF. An allomancer hovering in the air (whose push cancels out gravity) exerts an ANF equal to gravity back to their target. Theoretically, the Allomantic Normal Force could be greater than the Allomantic Force if the target accelerated in the opposite direction of the push. If you pushed (not pulled) on a target, and the target moved towards you (e.g. a very determined Steel Inquisitor, resisting your push and walking towards you), that normal force would push on you harder. This could result in “pushing matches” between Allomancers who try to move towards each other for even stronger pushes. Allomantic Normal Force works both ways. If the Allomancer is anchored (e.g. braced against a wall), the target will experience an Allomantic Normal Force. Other details: There are two main coins in Mistborn: Imperial boxings (gold) and clips (copper or bronze). In real life gold coins are usually around 30 grams, but I’ve experimented with increasing their mass by about 10-100 times for the game. Currently, I’ve kept them as 30g. When pushed with any reasonable force, 30g coins instantly fly off of the screen like bullets. There’s no user feedback that they pushed on that coin, other than, “that coin no longer appears to exist.” If you drop a coin from the air, it is on the ground by the next frame. Coins are sometimes described as behaving like bullets, but I don’t like how that works in the game. With heavier coins, you can see the coin after you push on it, but it still moves very quickly. Another option (which is the one I’m using in the game) is to simply cap their maximum velocity. I’ve left it at around 120m/s, which feels good. That’s about 1/3 the speed of sound. It causes some problems with calculating the Allomantic Normal Force from the target, but those have been resolved with coding (more or less). The image on the coins in the game is taken from Shire Mint. Fun fact: Unity doesn’t let you modify force vectors individually, which makes this a bit hard. You can only add forces/accelerations/velocity changes one at a time, then they are all applied to the object at the end of the frame. Calculating the Allomantic Normal Force is absolutely disgusting. See my code on GitHub, if you’re curious. I hope you all enjoyed the read! Please discuss this and give your opinions on the physics and maths of Allomancy. Specifically, Are there any more elegant relationships between Allomancer/target mass and Allomantic Force that you think I should try? Does anyone have any esoteric knowledge of Unity’s Rigidbody/Force systems that you think could be helpful? Any general ideas for the game? Any suggestions from what you can see in the videos? Any spelling/formatting issues with the post? Thank you.
- 37 replies
-
17
-
- physics
- steelpushing
-
(and 3 more)
Tagged with:
-
Update 1.2.1 – The Zinc Peripheral In Invested 1.2.1, the sphere's had a zinc peripheral installed, letting it use feruchemical zinc to increase its processing speed and slow down time. This makes it easier to fire coins while flying and select targets for Pushing and Pulling in the heat of the moment. See the changelog for all changes, but here's one in particular: you don't have to select targets before Pushing or Pulling on them. Trying to Push with no targets selected will Push on whatever metal you're looking at (dubbed "vacuous" Push/Pulling). This means you can fly around Luthadel without touching the keyboard. Since some of the controls have changed, be sure to check the in-game Help Overlay as a refresher. Next step: Means of quickly choosing different methods of controlling Pushes and Pulls. One of these will be a method for Pushing on all targets in a general direction, which Wax does a lot in the books. Another is the famous steel bubble. If math gets anyone excited, here's the fun differential equation I wrote for the intensity of the visual effect during zinc time. Fiddle with the variables and try to figure out what they're for, 'cause I ain't telling. X-axis is percentage of zinc remaining in the bank, and y-axis is intensity. Hope everyone's having a good summer. As always, let me know your thoughts. Update 1.2 Last year, I began working on a game/simulation implementing the magic system of Allomancy. I made a thread several months ago to document the initial state of the game and discuss different ways to mathematically model Pushing and Pulling. I establish a lot of the physics of the game there, so I recommend you read it if you haven't already. I've worked on the project a lot over the past few months. This post will be separated into three main sections: the first, focusing on the physics; the second, focusing on the game (with an interlude for more physics); and my plans for the future. Here is the second update on the progress of Invested. The Physics In Pagerunner's famous thread, I made several simulations comparing different models of Pushing and Pulling, showing off how Pushing duels could work as well as what happens when the coin you're Pushing suddenly hits a solid wall/ground. Those simulations can be all viewed in-game, so feel free to examine them yourself and experiment with the Allomancy settings. If we assume anchors do nothing special for your Pushes, Allomancy behaves like an undamped spring. If you push off of a coin into the air, you'll oscillate up to your max height, then fall all the way back down to the ground, then back up, and so on. Changing the relationship between distance and strength doesn’t change the behavior of the system. Pushing duels work in a similar way. The 10 cubes are allomancers, anchored to the ground. Without any dampening, you get a boring spring. The only model I could find that solved both of these problems was the infamous theory that the strength of Pushes is a function of velocity. In case you haven't been following those conversations, this theory (in its most basic form) claims "the higher the relative velocity between the Allomancer and target, the weaker the Allomantic force." Pushes on anchored coins will be stronger than Pushes on unanchored coins because anchored coins are completely stationary (that is, the relative velocity between the Allomancer and target is much smaller). The flavor of this theory that works best in the game (in my opinion) reverses the effect when the relative velocity is negative, i.e. when the Allomancer and target are moving towards each other. This means that Pushes on targets flying towards you are even more stronger than Pushes on targets flying away from you. When you're falling and throw a coin down, your Push will be weak until the coin hits the ground. Then, your relative velocity will be negative, and the Allomantic force will increase significantly, giving you a "jolt" as soon as the coin hits. This is the effect we see in the books, so it's what I have enabled by default in the game. With this model, Allomancers stabilize near their maximum height, rather than oscillate about it: Changing the constant used in the calculation of this velocity factor makes the system more critically/under-damped: Watch how duels play out. I've also unanchored the Allomancers, and this looks a lot more like how I envision Pushing duels in the books. The strength of the Allomancer is important, but weight determines who will move in the end. Again, you can experiment with these settings at any moment. The Game The player is a "primer sphere" - an Allomechanical construct or fabrial. It is an experimental device designed to test the limits of Scadrian magic. The sphere's mechanical nature gives it full control of its body and moment, allowing it to roll across surfaces and jump. This is enhanced by the first metal the sphere can burn: pewter. This is used for sprinting and pewter-jumping. By passively burning pewter, the sphere exerts a greater force while moving, allowing it to better anchor itself or move while Pushing and Pulling. While burning pewter and jumping, the sphere jumps further in that direction and can jump off or up walls or kick away small objects. Secondly, the primer sphere can burn iron and steel. Passively burning either of these metals reveals all nearby sources of metals. The wider the line, the heavier the source. The brighter the line, the stronger the potential Push on that metal. The sphere can "Pull-target" and "Push-target" one or more metals at once. When a metal is Pull-targeted, it can be Pulled on - likewise for Push-targets and Pushing. (Interlude: physics) After all the calculations are done, the player has some Allomantic Force they exert on the target. The mass of iron or steel burned is directly proportional to the net force they exert. If you're pushing with 1000N of force, you're burning 1000mg, or 1g, of iron every second. There's actually a WoB that mildly contradicts this: according to Brandon, metal burning speed is proportional to power drawn, not force. There are two reasons for why I make burn rate proportional to force. First, I can't be sure if Brandon is talking about "power" with the definition used in physics (i.e. a change in energy over time). If not, then there's nothing to worry about; the novels are wobbly enough to not be sure how precisely metals are burned. Still, in the future, I might shift things around to have all calculations work around power/energy rather than force, but the former is harder to calculate than the latter. My college-level textbook only talks about power in regards to applying a force to an object such that it moves at a constant velocity, so the math would get… difficult. I'm working on a model called "Distributed Power" based off of Pagerunner's model 3 that does something similar to this, but it's a work in progress. The main difference between force and power (in this context) is that power is a function of velocity; but, if we're using the Exponential with Velocity model, force still changes with velocity, just with a different relationship. There's potential for a fair bit of discussion in regards to this. The second, more important reason for making burn rate a function of force is reduce obfuscation - if you're consistently Pushing with 1000N, you know you're losing exactly 1g of steel every second. If you have only 10g of steel left, your intelligent lizard brain can figure out how long you can keep up that push. This relationship is more intuitive for the player, and changing this to power would lose that clarity. (end interlude) It wouldn't be Mistborn if you couldn't throw coins. You can toss coins. If you Push while doing this, you'll fire coins directly towards the crosshair. Holding "jump" while tossing a coin will throw it downward, useful for cruising above the ground or a smooth landing. There's also a "Coinshot mode." With this, holding down Push (right-click) and pressing Pull (left-click) will instead throw a coin. This makes throwing coins work more like a conventional FPS where the LMB fires bullets. This (along with all of the controls, I guess) is a WIP. There are a few scenes for the player to play around in: a tutorial and several sandboxes (as well as the Sandbox, which has some fun zero-gravity targets). cracks knuckles cries in GTX 965M Turns On Motion Blur it's gamer time (recorded back when I only had my laptop at school) There is an assortment of other videos here. The Future We've talked a lot about Newton's third law a lot, but let's take a look at Sanderson's third law: "Expand on what you have already, before you add something new." Better ways of throwing coins Changing between semi-automatic and fully-automatic coin-throwing Throwing multiple coins in different patterns Oftentimes in the books, you see Mistborn throwing a "spray" of coins at an enemy like a shotgun blast. Pewter From the start, my plan with pewter was for it to work like a shield in other games, where burning it will prevent you directly losing health. Once health actually becomes a thing, pewter will serve this purpose. HUD General polish is needed. It should be more clear when metal reserves are refilled, coins are picked up, on-screen text changes, etc. Sound The game's completely mute at the moment. I have little experience with sound design and production, so having a meaningful sound system is still a ways away. Controls I've been living in my own bubble, so I've grown accustomed my choice in keybinds. I am absolutely certain think that they're not the most intuitive. If you play the game, please let me know which controls make sense and which ones don't. Argent threw in the idea of using bullet time (or, perhaps, Feruchemical zinc time) for steel and iron. It would help a lot to make Pushing, Pulling, and target selection easier. In general, make target selection better. When you're surrounded by metal objects, there is a lot of visual clutter on the screen. I need to make a better system of prioritizing target selection so that you can say "I want to choose this target" and not accidentally select a target in front of or behind it. I definitely plan on adding macros/techniques for Pushing and Pulling. Vin's Horseshoe Wheel is one example. What I call the "centrifuge" is another - Pulling an object such that it orbits around your body, then releasing it such that it flies in the targeted direction. Lurchers never got their fair share of offensive combat in the books, so I want to show how formidable they can be, with a spicy little feedback loop or two. Other Allomantic metals Tin: zooming in, informative HUD elements about the environment, dispelling mists/visible stars in Luthadel. Bronze: see nearby sources of kinetic Investiture, such as puzzle elements or enemies that would try to Push on you. My requests for you: Play the game! You can download it from my GitHub. What controls make the most sense for you? What bugs and physics kinks do you find? Sanderson's 0th law says to err on the side of awesome. What should I add that would be fun? Mistborn is a fantasy novel, after all - so what are your fantasies for Allomancy in a game?
- 22 replies
-
34
-
Recently, I wanted to create a fantasy world setting with two moons. And, of course, because I’m a complete mathochist, I decided to have a theoretically possible solar system in which to create this. This lead down the rabbit hole, and I got to have a long worldbuilding session (actually several) to create this world, with some pretty amazing results. So, I figure, why not go over this whole process on these forums? I’ll go into it in detail, explaining as much as I can, but I’ll leave markings if you don’t want to go through all the hard work. IMPORTANT NOTE: Whenever I mention something like ‘full moon’ or ‘equinox’, I’m not refer to the day, I’m referring to the precise position which occurs in an instant. Keep this in mind. WARNING! GEOMETRY AHEAD! SKIP TO WHERE THERE’S MORE CAPITAL LETTERS TO AVOID! Earth has one moon, but, like all orbiting bodies it follows very specific rules, known as Keplerian geometry. There are a few rules to Keplerian geometry, but (for now) we’re just interested in the one which states that all orbiting bodies orbit in an ellipse with two foci. All planets must have the star they’re orbiting around as a focus point, consequently, all moons have the planet they’re orbiting as a focus point. That’s good. All Kelplerian orbits have 5 points known as Lagrangian points. These are fixed points in which objects can be placed to have stable orbits. In relation to the Earth and its Moon, they are as follows: L1 is between the Moon and Earth. L2 is on the far side of the Moon, lining up with the Earth (though not with the Sun, because the Moon orbits the Earth). L3 is the far side of the Moon’s orbit. L4 and L5 are 60 degrees off in the orbit, ahead and behind respectively. (Yes, L4 and L5 are slightly more complicated than that, but that isn’t needed now). I do know (some of) the physics behind it, but that’s a bit off-topic right now. So, it seems that, to have two Moons, we just have to put a Moon on the L3 point, right? Wrong. Because L1, L2, L3 are all unstable points. Can’t put stuff of any decent size mass there. I mean, theoretically, you might be able to put very small mass objects in L3, (like, say, an artificial satellite) but we’d have to resort to magic rock to have a Moon-sized object. So that’s out. We can put a Moon in the L4/5 spot, but I’d rather avoid that because I like the thematic idea of opposite Moons. So, suppose we avoid Lagrangian points, and just have two Moons in the same orbit, opposite each other. Does that work? Yes. And no. The L3 points aren’t enough to keep it in balance, so, (as best as I can figure, and I’m not an astrophysicists) it would need to be perfect placed to avoid them accelerating towards each other due to gravitational forces. A solution, sure, but it’s inelegant and isn’t likely to ever occur naturally. Instead, I decided to follow the binary approach, as in, ‘binary star system’. Binary stars orbit each other (oddly enough) sharing one focus point, while having the other one opposite each other. And, since the Earth is a focus point, we can have two moons orbiting it similar to a binary star system’s. Solved! END OF GEOMETRY SECTION! Long story short, we can two moons orbiting a planet opposite each other. We’re going to assume that the orbital period is exactly 28 days (synodic orbit), because it makes my life easier. (You’ll notice I’m about to make a lot of these assumptions) Now, I could go through the complete lunar calendar with respective positions, but seems like work which doesn’t involve math or writing, so instead, I’ll just list a quick set of rules to follow. 1. There will always be a total of a full moon, if you add the two moons together. 2. Draw the two moons in orbit around the planet. Draw a line between them so it looks like a ‘divide’ symbol. The respective moons can only be seen by people from their side of the planet, both can be seen while on the line itself. The moons can only be seen at night, though. 3. The moon which can only be seen in the beginning of the night is the waxing moon. The moon which is seen after midnight is waning. 4. Once every two weeks is full moon, swapping moons. Once every other series of two weeks is perfect half-moons, swapping waning and waxing Are we done? Hah! As I said, I’m a mathochist, and, what’s more, I’m a Julian-loving mathochist at that. I haven’t even started. Because now that we’ve gotten the moon out of the way, let’s talk about the planet. MORE GEOMETRY! IT’S FUN, I PROMISE! Kepler’s Law of Orbital Motion states that planets have a constant area speed. In other words, time it takes to cover a portion of the orbit such that it has area n between the start point, end point, and the sun (as a triangle, of sorts) is the same time it takes to cover any other points with the same area. Or, bluntly, area = time. (Not entirely right, but right enough for this discussion.) Equinoxes and solstices are caused by the tilt in the Earth’s spin which is completely independent from the elliptical orbit. Equinoxes are when the tilt is in a tangent to the Earth’s orbit to the Sun, solstices are when it is either pointing towards the Sun or away from it. Equinoxes have equal 12 hour day/night, solstices have longest day or longest night (summer, winter respectively). This is important because of the equinoxes and the solstices. Since these occur at 90 degrees from each other, we can adjust the time between solstices and equinoxes by moving the free focus point around and mucking around with length and width of the ellipse. (If you want to draw a diagram, draw a plus. The center of the plus is the sun. Draw an ellipse, with one focus being the center of the plus. Where the lines of the plus and the ellipse lines meet are the solstices and equinoxes.) Time adjustment to is possible, but it is complicated, so let’s move on. I’m just going to assume all the finite little adjustments I’m about to mention is possible because I think it is and because even I have my limits when it comes to this stuff. Calendar math is just a hobby. AND WE’RE ALL DONE WITH GEOMETRY! COME BACK, PLEASE! Now, this section requires some math. You can’t skip it, because this is necessary for orbital calculations. Promise. (Well, okay, you can skip to the last three paragraphs, but come on! It’s calendar math. Why would you want to skip it?) (No seriously. Don’t skip if you want to learn how to do this yourself.) So, let’s say we make the year 364 days, exactly 6 hours. (cough can’t imagine why I’d do that cough) That means (aside from needing a leap year precisely every four years, but see the note on that later) the solstice would move six hours, and we’d have a total of 13 28-day months. What does this mean? Well, let’s assume the winter solstice occur at precisely 1200 hours the first year. At Year+1, it will occur at precisely 1800 hours. At Year+2, it will occur at 2400, Year+3 0600, Year+4 back to 1200 and the cycle repeats. Same for the others. Now it’s easy to see why time adjustment between the equinoxes and solstices are necessary. There are 13 lunar months. If there is an equal amount of time between solstices + equinoxes, only one solstice/equinox can fall out during a full moon. If, say, the distance between them is 5-3-2-3 months (this is possible), they can all occur during a full moon, they just have variable time lengths between them. (In fact, the Earth’s distance between equinoxes is slightly off.) All’s well that ends well? Ha! Because, remember, the equinox progresses 6 hours per year (assuming the year cycle we established. Remember, you can whip up any numbers to your own liking) So, after a perfect solstice / full moon overlap, in 4 years, the full moon will have moved 1 day forward. In 28 years the full moon will have moved 1 week forward, and the winter equinox will now occur during perfect half-moons. In 56 years, we’ll be back at full moon, but with the other moon (remember, this planet has two moons) and in 112 years, it’ll be back where it started. All-in-all, I now have a 112-year lunar cycle calendar to use for my fantasy world. But wait! I was using the winter solstice in conjunction with the full moon as an example but we still have the summer solstice, vernal equinox, and autumnal equinox to use within our 112-year cycle. Can we have a system which only allows one full moon per year to coincide with one of the four? Yes, the easiest way to do this is to add a six-hour gap in the cycles, giving us 5-3-2-3, except each one also has six hours in addition to the months, but giving either the 5 or 2 an extra 12 hours after subtracting a day. (The math works, trust me on this. There may be other ways, but this is my way.) SUMMARY: So, every four years, the winter solstice, vernal equinox, summer solstice, autumnal equinox all swap between full moons, but these series of four years only occur every 28 years, but every cycle of 28 swaps between one of four options, (Full moon A, equal moons waning A, waxing B; Full moon B; equal moons waxing A, waning B; in that order unless I made a mistake) giving us a full cycle of 112 years total. Now, how does this cycle work when we have a specific 13-month calendar? Evil laugh. I thought you’d never ask. Since every four years adds a day, the calendar is moved one month every 112 years, if we don’t add leap days (which I don’t intend to). Which means, when a winter solstice occurs during a full moon during a specific month, that will not happen again for 1456 years. See? Math and world-building is fun. And, for those who remember me, I'm back. Nice to be here again.
-
Simply awesome.... I think we need a separate thread so everyone can get all their comments and math jokes out, and leave the ch 13-15 reaction thread for reactions. Personally I'm waiting to preorder my "Want to divide by zero?" t-shirt from brandon's site
-
Here are a couple of calculations I did about Roshar. The necessary variables (gravitational constant, radius) are from the AU essay. DISCLAIMER: I have little experience with astronomy, and these calculations may be wrong. Please submit any corrections, to improve the data. Roshar's mass: Gravitational constant = 70% of earth Radius = 90% of earth Mr = mass Roshar m*g=(G*Mr*m)/r^2 m*g*r^2=G*Mr*m g*r^2=G*Mr Mr=(g*r^2)/G Mr=((9.81*0.7)*(6.371*10^6*0.9)^2)/(6.673*10^-11) Mr=(6.867*3.288*10^13)/(6.673*10^-11) Mr=(2.258*10^14)/(6.673*10^-11) Mr=3.383*10^24 kg To calculate Roshar's orbit, and the mass of the sun I had to do something different. As I couldn't find any data on it on the internet I used the AU starmap. Here, the color of the sun is lighter than that of our sun, making it seem that it is of a higher spectral class (https://en.wikipedia.org/wiki/Stellar_classification#Harvard_spectral_classification). I then took the spectral classes above that of the sun (F till O) and created a tool that takes the highest and lowest luminosity, and then uses that to calculate the habitable zones. I then calculate what the mass of the star need to be to make Roshar have its period of 1.1 years and still fall in the habitable zone. the program repeats this till the mass of the star is also within the right class. The results are as followed: If you want to use the tool yourself, I attached the python file here: stellar_mass.py. This shows that Roshar's sun would probably have a mass of around 1.4 solar masses. this would mean that the semi-major axis of Roshar is: r=((G*M*T^2)/(4*pi^2))^(1/3) r=(((6.673*10^-11)*(2.8*10^30)*(3.15*10^7)^2)/(4*pi^2))^(1/3) r=((1.85*10^35)/(4*pi^2))^(1/3) r=(4.69*10^33)^(1/3) r=1.67*10^11 meter r=1.12 au (astronomical unit, earth's distance from the sun) I would also appreciate it if someone with more knowledge of astronomy looked over my calculations and my code, as I don't have much knowledge on the subject, and it is fairly possible I have made some mistakes.
-
I assume Every shard can combine with the regular 16 metals to form 16 new alomantic alloys (as can every shard combination because harmony and harmonium) then there are a total 1,048,576 possible alomantic metals and powers if all sixteen shards and their combinations are used. This includes the known god metals. this is based on the facts that: It has been confirmed by Brandon that what ruin is to atium, Honor is to shardblades Based on the formula File:Https://www.mathsisfun.com/combinatorics/images/cn.svg Where N is the number of shards and are can equal any whole number between 1 and 16 (sixteen shards) plus the additional non god metals as one more combination, the following determines the maximum number of allomantic alloys (65535 + 1) * 16 = 1,048,576
-
Last May, Tempus posted something that he/she called "Shardic Number Theory." Tempus included a section that discussed Bavadin (now known as Autonomy), the shard on Taldain, but had to censor most of the White Sand-Specific words. Here is the section: Bavadin - Five, Eight, Nine We don't know much about Bavadin, but there are a few options. There are five shshshshsh, and a shshshshsh can have five shshshshsh. The religious texts on shshshshsh are five hundred years old. There are eight shshshshsh, who elect eight shshshshsh, and shshshshsh spent eight years training. The shshshshsh religion sends eight shshshshsh at shshshshsh per day. There are also nine ranks of shshshshsh, nine people in shshshshsh's expedition, a maximum of nine shshsh without over-shshshshsh, and nine shshshshsh if you count the beggars. This paragraph brought to you by the Librarians. Now that we have a forum on which we can talk about white sand, who wants to fill this in? EDIT - I think that it was actually May 2014.





.thumb.jpg.6349608e38fc591142cdf6323d635d30.jpg)

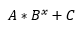
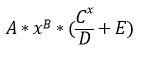
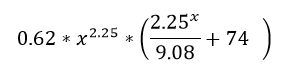


.thumb.png.637f0c632e7683978d3275dcc1dd1a68.png)
.thumb.png.21ae31552512ddb98621a9f821699bcc.png)
.thumb.png.eb36797d00031f16e1b5005dd7409e97.png)


.thumb.jpg.d618d64f5e470e32fd5394998cf4cc06.jpg)

